|
Size: 2550
Comment:
|
Size: 1112
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 5: | Line 5: |
| [[http://www.concepts.math.ethz.ch/doxygen/html/elasticity2D_tutorial_8cc-example.html| {{attachment:elasticity2D.png}} {{attachment:elasticity_solution.png}} ]] | Results obtained with the code described at page {{html/elasticity2D_tutorial_8cc-example.html}} of the [[Concepts/installation#Documentation|Doxygen documentation]]. {{attachment:elasticity2D.png}} {{attachment:elasticity_solution.png}} |
| Line 9: | Line 11: |
| [[http://www.concepts.math.ethz.ch/doxygen/html/exactDtN_8cc-example.html | {{attachment:exactDtN.png}}]] | Results obtained with the code described at page {{html/exactDtN_8cc-example.html}} of the [[Concepts/installation#Documentation|Doxygen documentation]]. |
| Line 11: | Line 13: |
| === Two dimensional meshes === [http://www.concepts.math.ethz.ch/doxygen/html/meshes_8cc-example.html <table frame="void" rules="none" border="0"> <tbody> <tr> <td><img width="204" alt="Graded mesh with quadrilaterals" src="http://www.concepts.math.ethz.ch/pics/trans-0.5-plainWR-mesh.png" title="Graded mesh with quadrilaterals" height="204" /></td> <td><img width="204" alt="Coarse mesh of a 2D L-shaped domain" src="http://www.concepts.math.ethz.ch/pics/mesh.png" title="Coarse mesh of a 2D L-shaped domain" height="204" /></td> <td><img width="204" alt="Mesh of a 2D L-shaped domain with corner refinement" src="http://www.concepts.math.ethz.ch/pics/lshape-mesh.png" title="Mesh of a 2D L-shaped domain with corner refinement" height="204" /></td> </tr> </tbody> </table>] |
{{attachment:exactDtN.png}} |
| Line 15: | Line 15: |
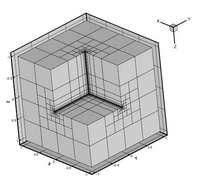
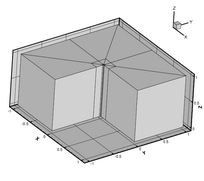
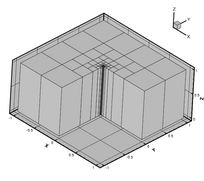
| === Three dimensional meshes === [http://www.concepts.math.ethz.ch/doxygen/html/meshes_8cc-example.html <table frame="void" rules="none" border="0"> <tbody> <tr> <td><img width="204" alt="Mesh of the Fichera corner" src="http://www.concepts.math.ethz.ch/pics/fichera-mesh.png" title="Mesh of the Fichera corner" height="181" /></td> <td><img width="204" alt="Coarse mesh of a 3D L-shaped domain" src="http://www.concepts.math.ethz.ch/pics/thickL015-mesh.png" title="Coarse mesh of a 3D L-shaped domain" height="181" /></td> <td><img width="204" alt="Mesh of a 3D L-shaped domain with corner refinement" src="http://www.concepts.math.ethz.ch/pics/thickL-mesh.png" title="Mesh of a 3D L-shaped domain with corner refinement" height="181" /></td> </tr> </tbody> </table>] |
== Two dimensional meshes == [[http://www.concepts.math.ethz.ch/doxygen/html/meshes_8cc-example.html]] |
| Line 19: | Line 18: |
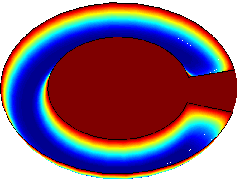
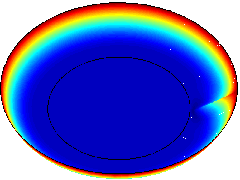
| === Magnetic field in a ring with a large (left) and a tiny (right) slit === <table cellspacing="1" cellpadding="0" frame="void" rules="none" border="1"> <tbody> <tr> <td><img width="240" alt="Magnetic field in a ring with a large slit" src="http://www.concepts.math.ethz.ch/pics/Slit_Large_thumb.png" title="Magnetic field in a ring with a large slit" height="180" /></td> <td><img width="240" alt="Magnetic field in a ring with a tiny slit" src="http://www.concepts.math.ethz.ch/pics/Slit_Tiny_thumb.png" title="Magnetic field in a ring with a tiny slit" height="180" /></td> </tr> </tbody> </table> |
{{attachment:trans-0.5-plainWR-mesh.png}} {{attachment:mesh.png}} {{attachment:lshape-mesh.png}} == Three dimensional meshes == [[http://www.concepts.math.ethz.ch/doxygen/html/meshes_8cc-example.html]] {{attachment:fichera-mesh.png}} {{attachment:thickL015-mesh.png}} {{attachment:thickL-mesh.png}} == Magnetic field in a ring with a large (left) and a tiny (right) slit == {{attachment:Slit_Large_thumb.png}} {{attachment:Slit_Tiny_thumb.png}} |
Gallery
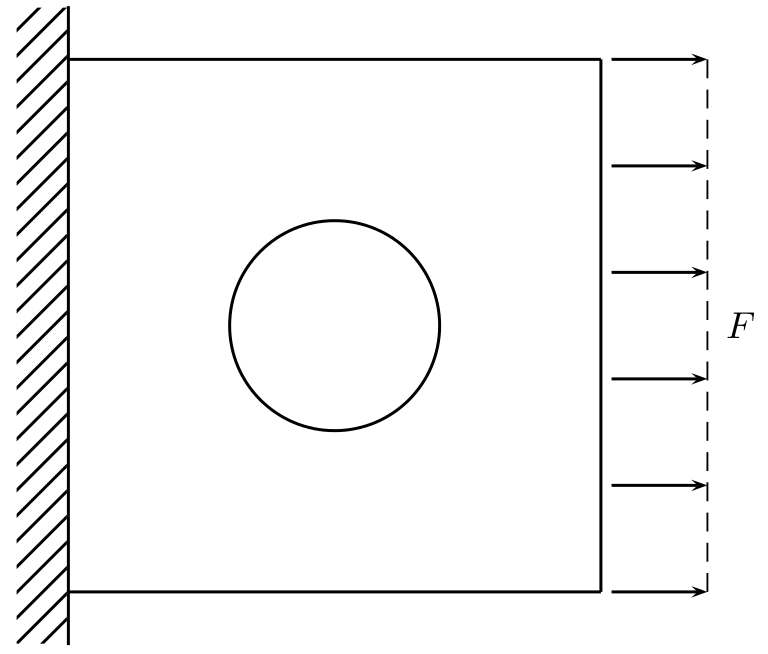
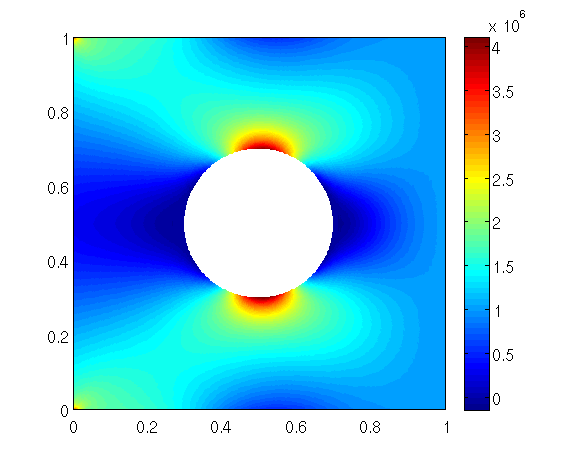
Elasticity in 2D
Results obtained with the code described at page of the Doxygen documentation.
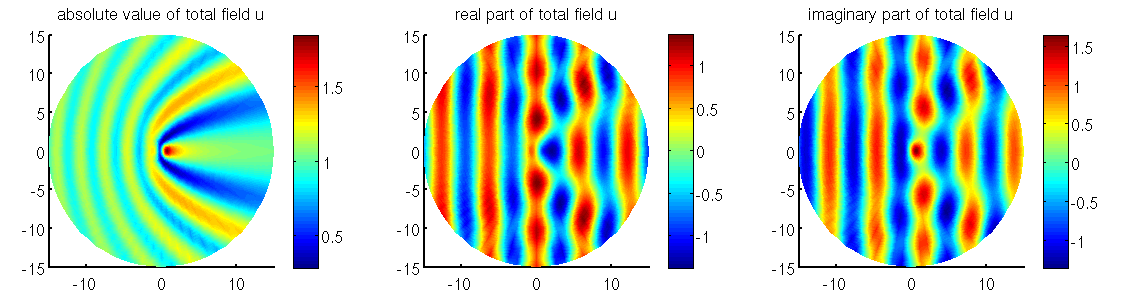
Transparent boundary conditions for scattering problems in 2D
Results obtained with the code described at page of the Doxygen documentation.
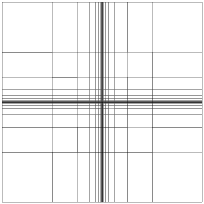
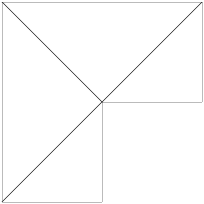
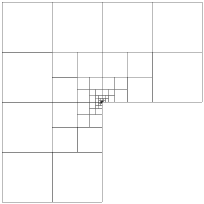
Two dimensional meshes
http://www.concepts.math.ethz.ch/doxygen/html/meshes_8cc-example.html
Three dimensional meshes
http://www.concepts.math.ethz.ch/doxygen/html/meshes_8cc-example.html
Magnetic field in a ring with a large (left) and a tiny (right) slit